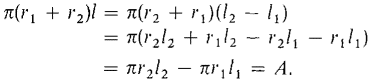Cylinders and Cones

When a curve in the plane is rotated about the x- or y-axis it forms a surface of revolution, as in Figure 6.4.1.

Figure 6.4.1 Surfaces of Revolution

The simplest surfaces of revolution are the right circular cylinders and cones. We can find their areas without calculus.

Figure 6.4.2 Cylinder

Figure 6.4.2 shows a right circular cylinder with height h and base of radius r. When the lateral surface is slit vertically and opened up it forms a rectangle with height h and base 2nr. Therefore its area is

lateral area of cylinder = 2πhr.

Figure 6.4.3: Cone

Figure 6.4.3 shows a right circular cone with slant height l and base of radius r.

When the cone is slit vertically and opened up, it forms a circular sector with radius l and arc length s = 2πr. Using the formula A = ½ sl for the area of a sector, we see that the lateral surface of the cone has area

lateral area of cone = πrl.

Figure 6.4.4: Cone frustum

Figure 6.4.4 shows the frustum of a cone with smaller radius r₁, larger radius r₂, and slant height l. The formula for the area of the lateral surface of a frustum of a cone is

lateral area of frustum = π(r₁ + r₂)l.

This formula is justified as follows. The frustum is formed by removing a cone of radius r₁ and slant height l₁ from a cone of radius r₂ and slant height l₂. The frustum therefore has lateral area

A = πr₂l₂ - πr₁l₁.

The slant heights are proportional to the radii,

so r₁l₂ = r₂l₁.

The slant height l of the frustum is

l = l₂- l₁.

Using the last two equations,