Region Between Two Curves - Solid of Revolution

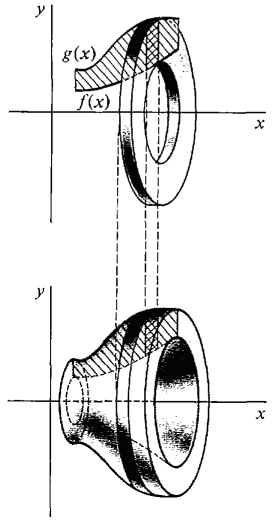
Now we consider the region R between two curves y = f(x) and y = g(x) from x = a to x = b. Rotating R about the x-axis generates a solid of revolution S shown in Figure 6.2.6(c).

Figure 6.2.6 (a): R₂, S₂

Figure 6.2.6 (b): R₁, S₁

Figure 6.2.6 (c) R = R₂ - R₁, S = S₂ - S₁

Let R₁ be the region under the curve y = f(x) shown in Figure 6.2.6(b), and R₂, the region under the curve y = g(x), shown in Figure 6.2.6(a). Then S can be found by removing the solid of revolution S₂ generated by R₁ from the solid of revolution S₂ generated by R₂. Therefore

volume of S = volume of S₂ - volume of S₁.

This justifies the formula

We combine this into a single integral.

VOLUME BY DISC METHOD

Another way to see this formula is to divide the solid into annular discs (washers) with inner radius f(x) and outer radius g(x), as illustrated in Figure 6.2.7.

Figure 6.2.7

Example 2