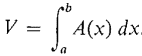Volume of a Solid

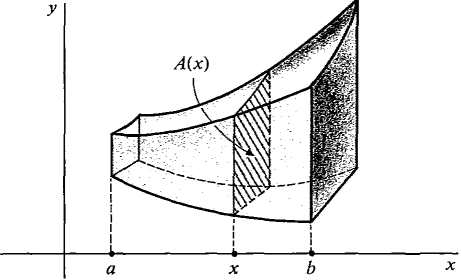
We now use the Infinite Sum Theorem to derive a formula for the volume of a solid when the area of each cross section is known. Suppose a solid S extends in the direction of the x-axis from x = a to x = b, and for each x the plane perpendicular to the x-axis cuts the solid in a region of area A(x), as shown in Figure 6.1.5. The area A(x) is called the cross section of the solid at x. The volume is given by the formula:

VOLUME OF A SOLID

Figure 6.1.5

JUSTIFICATION
Slice the solid S into vertical slabs of infinitesimal thickness Δx, as in Figure 6.1.6. Each slab, between x and x + Δx, has a face of area A(x),

Figure 6.1.6

and thus its volume is given by

ΔV ≈ A(x) Δx       (compared to Δx).

(The infinitesimal error arises because the area of the cross section changes slightly between x and x + Δx.) Then by the Infinite Sum Theorem,

The pattern used in justifying the two formulas in this section will be repeated again and again. First find a formula for an infinitesimal piece of volume ΔV. Then apply the Infinite Sum Theorem to get an integration formula for the total volume V.

Example 1: Pyramid

Example 2: Cylindrical Wedge