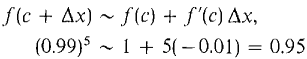| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Limits, Analytic Geometry, and Approximations Limits, Analytic Geometry, and Approximations  Derivatives and Increments Derivatives and Increments  Examples Examples  Example 3 Example 3 |
|






|
|
Example 3
Find an approximate value for (0.99)5. Let f(x) = x5, c = 1. Then f(c) = 15 = 1, f'(c) = 5c4 = 5. We put 0.99 = c + Δx, Δx = -0.01. Then the approximate value is
To get an error estimate we see that f"(u) = 20u3, so |f"(u)| ≤ 20 for u between 0.99 and 1. Then M = 20, and
or 0.949 ≤ (0.99)5 ≤ 0.951. Theorem 1 is closely related to the Increment Theorem in Section 2.2. The relation between them can be seen when we write them next to each other.
|
|
Home  Limits, Analytic Geometry, and Approximations Limits, Analytic Geometry, and Approximations  Derivatives and Increments Derivatives and Increments  Examples Examples  Example 3 Example 3 |
|
Last Update: 2010-11-25