| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Limits, Analytic Geometry, and Approximations Limits, Analytic Geometry, and Approximations  Derivatives and Increments Derivatives and Increments  Examples Examples  Example 1 Example 1 |
|||||||||||||||||||||||||||||
| See also: Example 1 (Concluded) | |||||||||||||||||||||||||||||






|
|||||||||||||||||||||||||||||
Example 1
Consider the curve f(x) = x1/3. Then f'(x) = ⅓x-2/3. At the point x = 8, we have x = 8, f(x) = 2, f'(x) = 1/12 = 0.0833 .... Thus
This is the slope of the line tangent to the curve at the point (8,2). As Δx approaches zero, the slope of the secant line through the two points (8, 2) and (8 + Δx, (8 + Δx)1/3) will approach 1/12. We make a table showing the slope of the secant line for various values of Δx.
|
|||||||||||||||||||||||||||||
Home  Limits, Analytic Geometry, and Approximations Limits, Analytic Geometry, and Approximations  Derivatives and Increments Derivatives and Increments  Examples Examples  Example 1 Example 1 |
|||||||||||||||||||||||||||||
Last Update: 2010-11-25


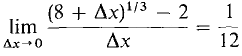
 = slope of secant line
= slope of secant line