Hyperbolas

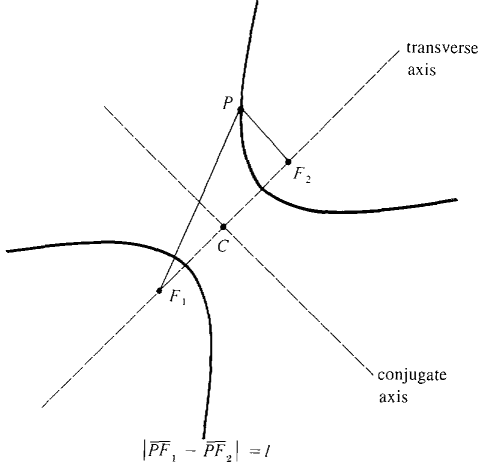
We turn next to the hyperbola. A hyperbola, like an ellipse, has two foci. However, the distances between the foci and a point on the hyperbola must have a constant difference instead of a constant sum.

In this definition, l must be a positive number less than the distance between the foci. A hyperbola will have two separate branches, each shaped like a rounded V. On one branch the points are closer to F₁ than F₂; and on the other branch they are closer to F₂ than F₁ Figure 5.5.6 shows a typical hyperbola. The path of a comet on an orbit that will escape the solar system is a hyperbola with the sun at one focus. The shadow of a cylindrical lampshade on a wall is a hyperbola (the section of the light cone cut by the wall).

The line through the foci is the transverse axis of the hyperbola, and the point on the axis midway between the foci is the center. The hyperbola crosses the transverse axis at two points called the vertices. The line through the center perpendicular to the transverse axis is the conjugate axis. The hyperbola never crosses its conjugate axis. A hyperbola is symmetric about both axes. A simple equation is obtained when the transverse and conjugate axes are chosen for the coordinate axes.

Figure 5.5.6 Hyperbola