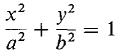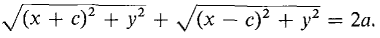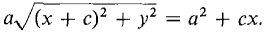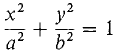The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages.

Home Limits, Analytic Geometry, and Approximations Ellipses and Hyperbolas Theorem 1
 
del.icio.us Reddit Facebook StumbleUpon MySpace Twitter Search the VIAS Library  |  Index

Theorem 1

THEOREM 1

For any positive a and b, the graph of the equation

05_limits_g_approx-296.gif

is an ellipse with its center at the origin. There are three cases:

(i) a = b. The ellipse is a circle of radius a.

(ii) a > b. This is a horizontal ellipse, whose major axis is the x-axis, and whose minor axis is the y-axis. The length is 2a. The foci are at (-c, 0) and (c, 0), where c is found by

c2 = a2 - b2.

(iii) a < b. This is a vertical ellipse whose major axis is the y-axis and whose minor axis is the x-axis. The length is 2b. The foci are at (0, -c) and (0, c), where c is found by

c2 = b2- a2.

05_limits_g_approx-297.gif

Figure 5.5.2

This theorem is illustrated by Figure 5.5.2. Here is the proof in case (ii), a > b. A point P(x, y) is on the ellipse with foci (-c, 0), (c, 0) and length 2a if and only if the sum of the distances from P to the foci is 2a. That is,

05_limits_g_approx-298.gif

Rewrite this as

05_limits_g_approx-299.gif

Square both sides:

05_limits_g_approx-300.gif

Simplify:

05_limits_g_approx-301.gif

Square both sides again:

a2(x2 + 2cx + c2 + y2) = a4 + 2a2cx + c2x2.

Collect the x2 and y2 terms and simplify.

x2(a2 - c2) + y2(a2) = a4 - a2c2 = a(a2 - c2).

Using the equation

b2 = a2 - c2,

write this as

x2b2 + y2a2 = a2b2.

Finally, divide by a2b2 to obtain the required equation

05_limits_g_approx-302.gif
Home Limits, Analytic Geometry, and Approximations Ellipses and Hyperbolas Theorem 1

Last Update: 2006-11-05