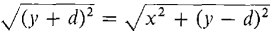The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages.

Home Limits, Analytic Geometry, and Approximations Parabolas Theorem 1
 
del.icio.us Reddit Facebook StumbleUpon MySpace Twitter Search the VIAS Library  |  Index

Theorem 1

Example 1: Vertical Parabola

The equation of a parabola is particularly simple if the coordinate axes are chosen so that the vertex is at the origin and the focus is on the y-axis. The parabola will then be vertical and have an equation of the form y = ax2.

THEOREM 1

The graph of the equation

y = ax2

(where a ≠ 0) is the parabola with focus F(0, ža) and directrix y = -(ža). Its vertex is (0, 0), and its axis is the y-axis.

PROOF

Let us find the equation of the parabola with focus F(0, d) and directrix y = -d, shown in Figure 5.4.7.

Our plan is to show that the equation is y = ax2 where d = ža. Given a point P(x, y), the perpendicular from P to the directrix is a vertical line of length 05_limits_g_approx-257.gif. Thus

distance from P to directrix =05_limits_g_approx-258.gif

Also,

distance from P to focus =05_limits_g_approx-259.gif

The point P lies on the parabola exactly when these distances are equal,

05_limits_g_approx-260.gif

05_limits_g_approx-261.gif

Figure 5.4.7

Simplifying we get

05_limits_g_approx-262.gif

Putting a = žd, we have d = ža where y = ax2 is the equation of the parabola.

Note that if a is negative, the focus will be below the x-axis and the directrix above the x-axis.

Example 2: Finding focus and directrix

Home Limits, Analytic Geometry, and Approximations Parabolas Theorem 1

Last Update: 2006-11-05