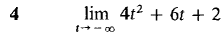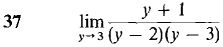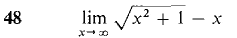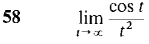| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Limits, Analytic Geometry, and Approximations Limits, Analytic Geometry, and Approximations  Infinite Limits Infinite Limits  Problems Problems |
|






|
|
Problems For Section 5.1
Find the following limits. Your answer should be a real number, ∞, -∞, or "does not exist."
69 Prove that if limx→c f(x) = ∞ then limx→c 1/f(x) = 0. 71 Prove that if limx→c f(x) = 0 and f(x) > 0 for all x, then limx→c 1/f(x) = ∞. 72 Prove that if limx→c f(x) exists or is infinite, then limx→0+ f(x) = limt→∞ f(1/t). 73 Prove that if limx→∞ f(x) exists or is infinite then limx→∞ f(x)= limt→0+ f(1/t).
|
|
Home  Limits, Analytic Geometry, and Approximations Limits, Analytic Geometry, and Approximations  Infinite Limits Infinite Limits  Problems Problems |
|
Last Update: 2006-11-25