| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Integral Integral  Numerical Integration Numerical Integration  Extra Problems Extra Problems |
|






|
|
Extra Problems
1 Evaluate 2 Evaluate 3 Evaluate 4 Evaluate 5 If F'(x) = l/(2x - 1)2 for all x 6 If G'(t) = 7 A particle moves with velocity 8 A particle moves with velocity 9 A particle moves with velocity v = (t + l)(2t + 3). If it has position y0 = 0 at time t = 0, find its position at time t = 10. 10 A particle moves with acceleration a = 1/t4. If it has velocity v0 = 4 and position y0 = 2 at time t = 1, find its position at time t = 3. 11 Find the area of the region under the curve y = 1/√x, 1 ≤ x ≤ 4. 12 Find the area of the region under the curve y = √x - x√x, 0 ≤ x ≤ 1. In Problems 13-30, evaluate the integral. 13 15 17 19 21 23 25 27 29 31 Differentiate 32 Differentiate 33 Differentiate 34 Differentiate 35 Find the function F such that F'(x) = x - 1 for all x, and the minimum value of F(x) is b.. 36 Find the function F such that F"(x) = x for all x, F(0) = 1, and F(l) = 1. 37 Find the function F such that F"(x) = 6 for all x, F(x) has a minimum at x = 1, and the minimum value is 2. 38 Find all functions F such that F"(x) = 1 + x-3 for all positive x. 39 Find the function F such that 40 Find the value of b such that the area of the region under the curve y = x{b - x), 0 ≤ x ≤ b, is 1. 41 Suppose f is increasing for a ≤ x ≤ b, and Δx = (b - a)/n where n is a positive integer. Show that 42 Suppose f is continuous for a ≤ x ≤ b. Show that 43 44 Evaluate 45 Find 46 Suppose f(t) is continuous for all t and let 47 Prove that for any continuous functions f and g, 48 Prove Schwartz' Inequality, 49 Suppose f is continuous and dx is positive infinitesimal. Show that 50 Suppose f is continuous, n is an integer, and dx is positive infinitesimal.
Prove that
|
|
Home  Integral Integral  Numerical Integration Numerical Integration  Extra Problems Extra Problems |
|
Last Update: 2010-11-26






 1/2, find F(2) - F(l).
1/2, find F(2) - F(l). for all t > - 1/4, find G(2) - G(0).
for all t > - 1/4, find G(2) - G(0). . How far does it move from times t0 = 1 to t1 = 5?
. How far does it move from times t0 = 1 to t1 = 5? . How far does it move from times t0 = 1 to t1 = 4?
. How far does it move from times t0 = 1 to t1 = 4? 14
14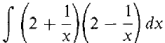
 16
16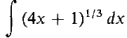
 18
18
 20
20
 22
22
 24
24
 26
26
 28
28
 30
30




 and F(0) = 1.
and F(0) = 1.

 Find the area of the top half of the ellipse x2/a2 + y2/b2 = 1 using the formula
Find the area of the top half of the ellipse x2/a2 + y2/b2 = 1 using the formula using the formula
using the formula 

 Prove that G"(x) = f(x).
Prove that G"(x) = f(x). Hint: Use the preceding problem.
Hint: Use the preceding problem. Hint: For each positive real c,
Hint: For each positive real c,  Use this to show that
Use this to show that 

