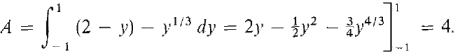Example 3: Area Below A Curve And A Line

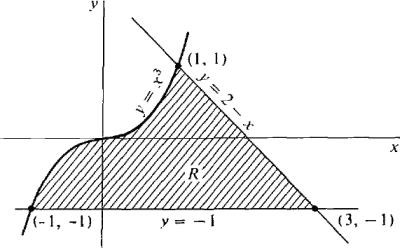
Find the area of the region R bounded below by the line y = - 1 and above by the curves y = x³ and y = 2 - x. The region is shown in Figure 4.5.6.

Figure 4.5.6

This problem can be solved in three ways. Each solution illustrates a different trick which is useful in other area problems. The three corners of the region are:

(- 1, - 1),           where y = x³ and y = -1 cross.

(3, - 1),           where y = 2 - x and y = - 1 cross.

(1, 1),               where y = x³ and y = 2 - x cross.

Note that y = x³ and y = 2 - x can cross at only one point because x³ is always increasing and 2 - x is always decreasing.

FIRST SOLUTION

Break the region into the two parts shown in Figure 4.5.7: R₁ from x = - 1 to x = 1, and R₂ from x = 1 to x = 3. Then

area of R =area of R_t + area of R₂.

area of R₁ = = 2.

area of R, == 2.

area of R = 2 + 2 = 4.

Figure 4.5.7

SECOND SOLUTION

Form the triangular region S between y = -1 and y = 2 - x from -1 to 3. The region R is obtained by subtracting from S the region S₁ shown in Figure 4.5.8. Then

area of R = area of S - area of S₁

area of R = 8 - 4 = 4.

.

Figure 4.5.8

THIRD SOLUTION

Use y as the independent variable and x as the dependent variable. Write the boundary curves with x as a function of y.

y = 2 - x becomes x = 2 - y.

y = x³  becomes x = y^1/3.

The limits of integration are y = - 1 and y = 1 (see Figure 4.5.9). Then

Figure 4.5.9

As expected, all three solutions gave the same answer.