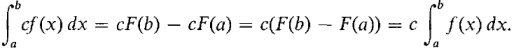| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |
|
Home  Integral Indefinite Integrals Integration Constant |
|||||||||
 Search the VIAS Library | Index
|
  |
||||||||
Integration Constant
THEOREM 3 Suppose the domain off is an open interval I and f has an antiderivative. Let P(x0, y0) be any point with x0 in I. Then f has exactly one antiderivative whose graph passes through P. PROOF Let F be any antiderivative of f Then F(x) + C is the family of all anti derivatives. We show that there is exactly one value of C such that the function F(x) + C passes through P(xo,yo) (Figure 4.3.2). We note that all of the following statements are equivalent: (1) F(x) + C passes through P(x0,y0). (2) F(x0) + C = y0. (3) C = y0 = F(x0). Thus y0 - F(x0) is the unique value of C which works.
Figure 4.3.2 The Fundamental Theorem of Calculus, part (ii), may be expressed briefly as follows, wheref is continuous on I. If
For evaluating definite integrals we introduce the convenient notation
It is read "F(x) evaluated from a to b." The Constant and Sum Rules hold for definite as well as indefinite integrals: Constant Rule
Sum Rule
The Constant Rule is shown by the computation
The Sum Rule is similar.
|
|||||||||
| Home Integral Indefinite Integrals Integration Constant |
|
||||||||
f(x)dx = F(x) + C,then
Last Update: 2006-12-01