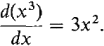Introduction

The Fundamental Theorem of Calculus shows that every continuous function f has at least one antiderivative, namely . Actually, f has infinitely many antiderivatives, but any two antiderivatives off differ only by a constant. This is an important fact about antiderivatives, which we state as a theorem.

Discussion:

Parts (i) and (ii) together show that if we can find one antiderivative F(x) of f(x), then the family of functions

F(x) + C, C = a real number

gives all antiderivatives of f(x). We see from Figure 4.3.1 that the graph of F(x) + C is just the graph of F(x) moved vertically by a distance C. The graphs of F(x) and F(x) + C have the same slopes at every point x. For example, let f (x) = 3x². Then F(x) = x³ is an antiderivative of 3x² because

But x³ + 6 and x³ - √2 are also antiderivatives of 3x². In fact, x³ + C is an antiderivative of 3x² for each real number C. Theorem 1 shows that 3x² has no other antiderivatives.

Figure 4.3.1

Part (ii) follows from a theorem in Section 3.7 on curve sketching. If a function has derivative zero on I, then the function is constant on I. The difference F(x) - G(x) has derivative f(x) - f(x) = 0 and is therefore constant. We used this fact in the proof of the Fundamental Theorem of Calculus.