Area of a Semicircle

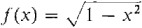Let , defined on the closed interval I = [-1,1]. The region under the curve is a semicircle of radius 1. We know from plane geometry that the area is π/2, or approximately 3.14/2 = 1.57. Let us compute the values of some Riemann sums for this function to see how close they are to 1.57. First take Δx = ½ as in Figure 4.1.10(a). We make a table of values.

The Riemann sum is then

Next we take Δx = 1/5. Then the interval [-1,1] is divided into ten subinter-vals as in Figure 4.1.10(b). Our table of values is as follows.

Figure 4.1.10

The Riemann sum is

Thus we are getting closer to the actual area π/2 ~ 1.57.

By taking Δx small we can get the Riemann sum to be as close to the area as we wish.