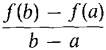| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Continuous Functions Continuous Functions  Properties of Continuous Functions Properties of Continuous Functions  Proof of the Mean Value Theorem Proof of the Mean Value Theorem |
|






|
|
Proof of the Mean Value Theorem
PROOF OF THE MEAN VALUE THEOREM Let m be the average slope, m = (f(b) - f(a))/(b - a). The line through the points (a,f(a)) and (b,f(b)) has the equation l(x) = f(a) + m(x - a). Let h(x) be the distance of f(x) above l(x) h(x) = f(x) - l(x). Then h is continuous on [a, b] and has the derivative h'(x) = f'(x) - l'(x) = f(x) - m at each point in (a, b). Since f(x) = l(x) at the endpoints a and b, we have h(a) = 0, h(b) = 0. Therefore Rolle's Theorem can be applied to the function h, and there is a point c in (a, b) such that h'(c) = 0. Thus 0 = h'(c) = f'(c) - l'(c) = f'(c) - m, whence f'(c) = m. We can give a physical interpretation of the Mean Value Theorem in terms of velocity. Suppose a particle moves along the y-axis according to the equation y = f(t). The average velocity of the particle between times a and b is the ratio
of the change in position to the time elapsed. The Mean Value Theorem states that there is a point of time c, a < c < b, when the velocity f'(c) of the particle is equal to the average velocity between times a and b.
|
|
Home  Continuous Functions Continuous Functions  Properties of Continuous Functions Properties of Continuous Functions  Proof of the Mean Value Theorem Proof of the Mean Value Theorem |
|
Last Update: 2006-11-05