| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |
|
Home  Continuous Functions Derivatives and Curve Sketching Changing of Curve Direction |
|
 Search the VIAS Library | Index
|
  |
Changing of Curve Direction
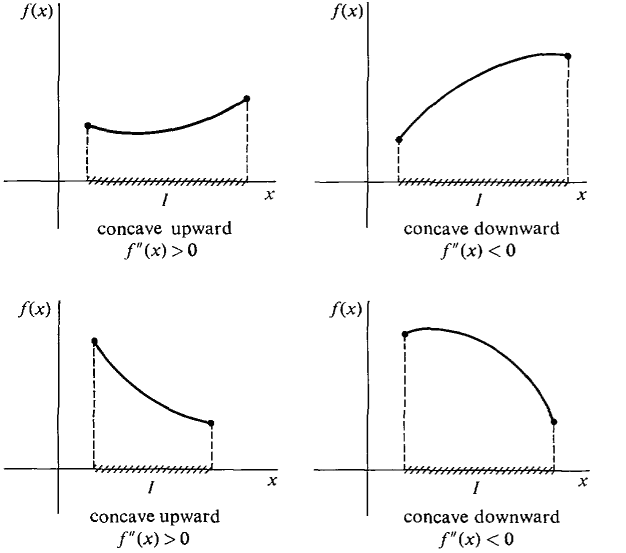
Let us now turn to the second derivative. It is the rate of change of the slope of the curve, so it has something to do with the way in which the curve is changing direction. When the second derivative is positive, the slope is increasing, and we would expect the curve to be concave upward, i.e., shaped like a ∪. When the second derivative is negative the slope is decreasing, so the curve should be shaped like ∩ (see Figure 3.7.4). A precise definition of concave upward or downward can be given by comparing the curve with the chord (straight line segment) connecting two points on the curve. DEFINITION Let f be defined on I. The curve y = f(x) is concave upward on I if for any two points x1 < x2 in I and any value of x between x1 and x2, the curve at x is below the chord which meets the curve at x1 and x2. The curve y = f(x) is concave downward on I if for any two points xx < x2 in I and any value of x between x1 and x2, the curve at x is above the chord which meets the curve at x1 and x2 (see Figure 3.7.5).
Figure 3.7.4
Figure 3.7.5
|
|
| Home Continuous Functions Derivatives and Curve Sketching Changing of Curve Direction |
|
Last Update: 2006-11-05