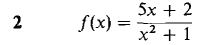Problems

In Problems 1-17, find the set of all points at which the function is continuous.

18             Show that f(x) = √x is continuous from the right at x = 0.

19            Show that f(x) = is continuous from the left at x = 1.

20            Show that f(x) = is continuous on the closed interval [-1, 1].

21            Show that f(x) = is continuous on the closed interval [0, 2].

22            Show that f(x) = ^! is continuous on the closed interval [-3, 3].

23            Show that f(x) = is continuous on the half-open intervals (-∞, -3] and [3, ∞).

24            Suppose the function f(x) is continuous on the closed interval [a, b]. Show that there is a function g(x) which is continuous on the whole real line and has the value g(x) = f(x) for x in [a, b].

25            Suppose lim_x→c f(x) = L. Prove that the function g(x), defined by g(x) = f(x) for x ≠ c and g(x) = L for x = c, is continuous at c.

26            In the curve y = f(x) illustrated below, identify the points x = c where each of the following happens:

(a)    f is discontinuous at x = c

(b)    f is continuous but not differentiate at x = c.