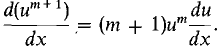The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages.

Home Differentiation Derivatives of Rational Functions Theorem 5: Power Rule
 
del.icio.us Reddit Facebook StumbleUpon MySpace Twitter Search the VIAS Library  |  Index

Theorem 5: Power Rule

THEOREM 5 (Power Rule)

Let u depend on x and let n be a positive integer. For any value of x where du/dx exists,

02_differentiation-109.gif

PROOF

To see what is going on we first prove the Power Rule for n = 1, 2, 3, 4. n = 1: We have un = u and u0 = 1, whence

02_differentiation-110.gif

n = 2: We use the Product Rule,

02_differentiation-111.gif

n = 3: We write u3 = u · u2, use the Product Rule again, and then use the result for n = 2.

02_differentiation-112.gif

n = 4: Using the Product Rule and then the result for n = 3,

02_differentiation-113.gif

We can continue this process indefinitely and prove the theorem for every positive integer n. To see this, assume that we have proved the theorem for m. That is, assume that

(1)

02_differentiation-114.gif

We then show that it is also true for m + 1. Using the Product Rule and the Equation 1,

02_differentiation-115.gif

Thus

02_differentiation-116.gif

This shows that the theorem holds for m + 1.

We have shown the theorem is true for 1, 2, 3, 4. Set m = 4; then the theorem holds for m + 1 = 5. Set m = 5; then it holds for m + 1 = 6. And so on. Hence the theorem is true for all positive integers n.
Home Differentiation Derivatives of Rational Functions Theorem 5: Power Rule

Last Update: 2006-11-06