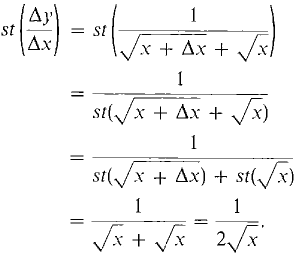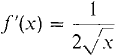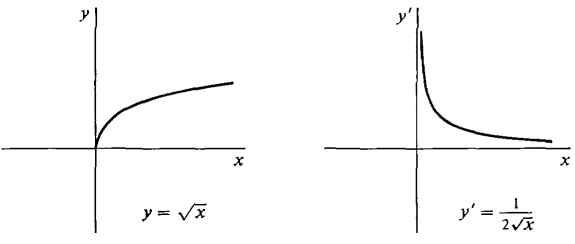| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Differentiation Differentiation  Derivatives Derivatives  Examples Examples  Example 2: Derivative of the Root-Function Example 2: Derivative of the Root-Function |
|






|
|
Example 2: Derivative of the Root-Function
Find f'(x) given f(x) = √x. Case 1
Case 2
Case 3
|
|
Home  Differentiation Differentiation  Derivatives Derivatives  Examples Examples  Example 2: Derivative of the Root-Function Example 2: Derivative of the Root-Function |
|
Last Update: 2010-11-25


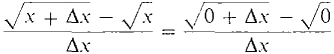
 is undefined. When Δx is a positive infinitesimal,
is undefined. When Δx is a positive infinitesimal,