| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Real and Hyperreal Numbers Real and Hyperreal Numbers  Infinitesimal, Finite and Infinite Numbers Infinitesimal, Finite and Infinite Numbers  Rules For Infinitesimal, Finite and Infinite Numbers Rules For Infinitesimal, Finite and Infinite Numbers |
||||||||||||||||||||||||||||||||||






|
||||||||||||||||||||||||||||||||||
Rules For Infinitesimal, Finite and Infinite Numbers
Assume that ε, δ are infinitesimals; b, c are hyperreal numbers that are finite but not infinitesimal; and H, K are infinite hyperreal numbers. (i) Real numbers:
(ii) Negatives:
(iii) Reciprocals:
(iv) Sums:
(v) Products:
(vi) Quotients:
(vii) Roots:
Notice that we have given no rule for the following combinations:
Each of these can be either infinitesimal, finite but not infinitesimal, or infinite, depending on what ε, δ, H, and K are. For this reason, they are called indeterminate forms. Here are three very different quotients of infinitesimals.
Table 1.5.1 shows the three possibilities for each indeterminate form.
Here are some examples which show how to use our rules.
The next three examples are quotients of infinitesimals.
|
||||||||||||||||||||||||||||||||||
Home  Real and Hyperreal Numbers Real and Hyperreal Numbers  Infinitesimal, Finite and Infinite Numbers Infinitesimal, Finite and Infinite Numbers  Rules For Infinitesimal, Finite and Infinite Numbers Rules For Infinitesimal, Finite and Infinite Numbers |
||||||||||||||||||||||||||||||||||
Last Update: 2006-11-15


 is infinitesimal.
is infinitesimal. is finite but not infinitesimal.
is finite but not infinitesimal.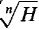 is infinite.
is infinite. is infinitesimal (equal to ε).
is infinitesimal (equal to ε).  is finite but not infinitesimal (equal to 1).
is finite but not infinitesimal (equal to 1). is infinite (equal to
is infinite (equal to  )
)