| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Real and Hyperreal Numbers Real and Hyperreal Numbers  Functions of Real Numbers Functions of Real Numbers  Problems Problems |
|






|
|
Problems
For each of the following functions (Problems 1-8), make a table showing the value of f(x) when x = -1, -½, 0, ½, 1. Put a * where f(x) is undefined. Example: 1 f(x) = x/3 2 f(x)=3 3 f(x) = 3x3 - 5x2 + 2 4 f(x) = 1/(x - 1) 5 f(x)= 6 f(x) = |x| 7 f(x) = |x-½| + |x + ½| 8 f(x) = 9 Is the set of ordered pairs {(3, 2), (0, 1), (4, 2)} a function ? 10 Is the set of ordered pairs {(0, 2), (3, 6), (3, 4)} a function ? 11 If f is the function f(x) = 1 + x + x2, find f(2), f(t), f(t + Δt), f(1 + t + t2), f(g(t)). 12 If f(x) = 1/x, find f(t), f(t + Δt), f(t2), f(1/t), f(g(0). 13 If f(x) = x 14 If f(x) = ax + b, find f(ct + d), f(t2), f(1/t), f(t/a), f(g(t)). For each of the following functions (Problems 15-20), find f(x + Δx) - f(x). 15 f(x) = 4x + 1 16 f(x) = x2 - x 17 f(x) = x-2 18 f(x) = x4 19 f(x) = √x 20 f(x) = 4 21 Find the domain of the function f(x) = 1/(x2 — 1). 22 Find the domain of the function f(z) = 23 What is the domain of the function f(x) = √x? 24 What is the domain of the function f(t) = 25 What is the domain of the function f(x) = 1/ 26 Show that if a and b have the same sign then |a + b| = |a| + |b|, and if a and b have opposite signs then |a + b| < |a| + |b|.
|
|
Home  Real and Hyperreal Numbers Real and Hyperreal Numbers  Functions of Real Numbers Functions of Real Numbers  Problems Problems |
|
Last Update: 2010-11-25



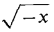

 , find f(t), f(t + Δt), f(t2),f(√t), f(g(t)).
, find f(t), f(t + Δt), f(t2),f(√t), f(g(t)).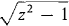
 ?
? ?
?