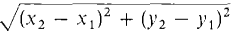| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Real and Hyperreal Numbers Real and Hyperreal Numbers  The Real Line The Real Line  Distance Between Two Points Distance Between Two Points |
|






|
|
Distance Between Two Points
In Figure 1.1.6, P(x1 y1) and Q(x2, y2) are two different points in the (x, y) plane. As we move from P to Q, the coordinates x and y will change by amounts that we denote by Δx and Δy. Thus change in x = Δx = x2 - x1, change in y = Δy = y2 - y1
Figure 1.1.6 The quantities Δx and Δy may be positive, negative, or zero. For example, when x2 > x1, Δx is positive, and when x2 < x1, Δx is negative. Using Δx and Δy we define the basic notion of distance. DEFINITION The distance between the points P(x1, y1) and Q(x2, y2) is the quantity distance (P, Q) = When we square both sides of the distance formula, we obtain [distance (P,Q)]2 = (Δx)2 + (Δy)2. One can also get this formula from the Theorem of Pythagoras in geometry: The square of the hypotenuse of a right triangle is the sum of the squares of the sides.
|
|
Home  Real and Hyperreal Numbers Real and Hyperreal Numbers  The Real Line The Real Line  Distance Between Two Points Distance Between Two Points |
|
Last Update: 2010-11-26



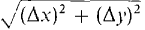 =
=