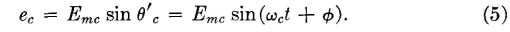Frequency and Phase Modulation

Several theoretical papers appeared on frequency modulation, notably in 1930 by van der Pohl,⁴⁰ and in 1931 by Roder.⁴¹ At about this time Armstrong did experimental work with frequency modulation. As a result, he was able to show that much reduction in received noise was possible if a rather large frequency deviation was used. His important 1936 paper⁴² on the subject initiated the practical development of frequency-modulation methods. In 1940 Everitt summarized existing knowledge and techniques.⁴³ The literature now contains much information on the subject.

Angle Modulation. Angle modulation includes both frequency and phase modulation, which are closely related. Angle modulation is defined² as "modulation in which the angle of a sine-wave carrier is the characteristic subject to variation." Much of the information that follows is summarized from the papers by Roder⁴¹ and Everitt.⁴³

The fact has been stressed that modulation is merely a process by which the message or program to be transmitted is translated, or moved, to a band in the radio-frequency spectrum. Also, it has been pointed out that the so-called carrier wave in no sense "carries" the signal to the distant station.

The definition² of phase modulation or PM is "angle modulation in which the angle of a sine-wave carrier is caused to depart from the carrier angle by an amount proportional to the instantaneous value of the modulating wave." The definition² of frequency modulation or FM is "angle modulation in which the instantaneous frequency of a sine-wave carrier is caused to depart from the carrier frequency by an amount proportional to the instantaneous value of the modulating wave."

To investigate phase and frequency modulation, assume that both a sinusoidal carrier wave and a sinusoidal modulating wave are impressed on a modulator that can cause amplitude, phase, or frequency modulation. The instantaneous value of the carrier voltage wave will be

and the instantaneous value of the voice-frequency modulating voltage wave will be

As has been explained, in amplitude modulation E_mc is caused to vary in accordance with the modulating frequency, and two sidebands, each containing the information to be transmitted, are created. A phase-modulated sinusoidal wave² is one "in which the argument contains a term whose wave form is similar to that of the signal to be transmitted." A frequency-modulated sinusoidal wave is one "in which the expression for instantaneous frequency contains a term whose wave form is similar to that of the signal to be transmitted." "The instantaneous frequency² of a sinusoidal wave whose argument is a function of time equals 1/(2π) times the derivative of the argument with respect to time."

Because in equation 3ω_c = 2πf_c, where f_c is the assigned carrier frequency and is a fixed value, this equation must be written in a more general form to show how phase and frequency modulation are accomplished. Thus,

In phase modulation, the angle φ is made to vary in accordance with the modulating signal. If m_p is the phase deviation, defined² as "the peak difference between the instantaneous angle of the modulated wave and the angle of the carrier," and is the maximum phase shift in radians produced by the sinusoidal modulating signal of equation 4, then the instantaneous value of a phase-modulated wave is

In frequency modulation, the instantaneous frequency of the output wave of the modulator must be caused by the modulating signal to vary about the average frequency f_c = ω_c./2π. The instantaneous frequency is by definition²

Thus, from equation 5,

Because ω_c is constant; the modulating wave must vary dφ/dt, and hence the instantaneous frequency is

where m_f is the frequency deviation and is² "the peak difference between the instantaneous frequency of the modulated wave and the carrier frequency." It has been called the frequency-modulation factor. From equations 8 and 9,

and integrating,

When this value is substituted in equation 5, the equation for a frequency-modulated wave becomes

Comparison of Phase and Frequency Modulation. It will be noted that equation 6 for a phase-modulated wave is very much like equation 12 for a frequency-modulated wave, the important difference being that in phase modulation the maximum phase shift during modulation is given by m_p and is independent of the modulating frequency, but in frequency modulation the maximum phase shift is given by what has been called the modulation index,^2,40,41 m_f/f_r, which varies inversely as the modulating frequency f_v. The ratio "of the maximum frequency deviation to the maximum modulating frequency of the system" is now called² the deviation ratio. In phase modulation, m_p is the maximum shift in phase that the audio signal of maximum intensity will cause, and, in frequency modulation, m_f is the maximum frequency shift that the audio signal of maximum intensity will cause. Accordingly, Roder stated⁴¹ that "frequency modulation corresponds to phase modulation where the amplitude of the audio signal is inversely proportional to frequency of that signal," A system of phase modulation will produce frequency modulation, or vice versa, if the modulating signal voltage is thus predistorted. Also, a system for demodulating frequency-modulated waves will demodulate phase-modulated waves, and vice versa, if after demodulation the wave is

Figure 22. An amplitude-modulated wave is shown above, and a frequency-modulated wave below. Each is modulated by a pure sine wave.

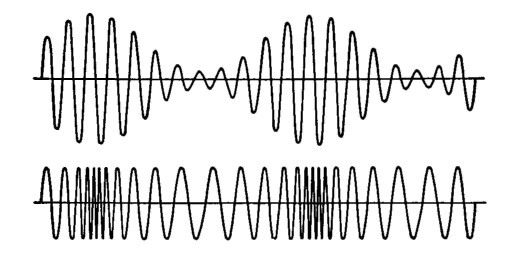
distorted. Another point brought out by Roder was that at corresponding intervals in amplitude modulation the carrier and sidebands are in phase, but in phase and frequency modulation, for small values of m_p and m_f/f_r, the carrier and sidebands are 90° out of phase.

The shapes of an amplitude-modulated wave and a phase or frequency-modulated wave are shown in Fig. 22. In phase modulation, the magnitude of the phase shift depends on the magnitude of the modulating signal, and the number of phase shifts per second depends on the frequency of the modulating signal. In frequency modulation, the magnitude of the frequency shift depends on the magnitude of the modulating signal, and the number of frequency shifts per second depends on the frequency of the modulating signal.

Sidebands were found to exist in an amplitude-modulated wave, and they also exist in a phase-modulated wave or frequency-modulated wave, but in greater number; in fact, in these two systems an infinite number of sidebands exist (at least theoretically). This is shown^41,43 by expanding equations 6 and 12 in accordance with the theory of Bessel's functions. Figure 23 has been prepared⁴³ in this manner.

It shows that for a frequency-modulated wave, because of ratio m_f/f_v previously mentioned, a high audio-frequency modulating signal does not cause so large a number of appreciable sidebands (or side-frequencies for a sinusoidal modulating wave) as is caused by a modulating wave of lower frequency. It should be noted_; however, that the overall bandwidth required in each instance is about the same and that it is wider than the maximum deviation in frequency for the high-frequency components of the audio-frequency modulating signal The practical significance is this: Modern frequency-modulation broadcast stations are adjusted for a maximum frequency deviation, or maximum change in frequency with the strongest modulating signal; of +/-75,000 cycles around the assigned carrier frequency which is for broadcast in the vicinity of 100,000,000 cycles. But the maximum bandwidth required to pass the sidebands of appreciable magnitude is about 200000 cycles wide. Thus, each frequency-modulation broadcast station is assigned a band in the frequency spectrum that is 200,000 cycles wide, and that is one important reason why frequency-modulation broadcasting is placed in the 100-megacycle region.

Figure 23. These figures show that frequency-modulated waves contain a large number of sidebands. Note that in frequency modulation the magnitude of the component of carrier frequency, fc, varies. (Adapted from reference 43.)

It is of interest to compare the bandwidth required for a phase-modulated wave and for a frequency-modulated wave. As Fig. 23 shows, for frequency modulation the bandwidth is about the same for any ratio of m_f/f_r. For comparable conditions, this is not true for a phase-modulated signal; for, as equation 6 indicates, the shift in phase is not inversely proportional to the modulating frequency. Thus, a phase-modulated signal will cover a much wider frequency band than a frequency-modulated signal will under comparable conditions. Frequency modulation is extensively used in practice, and phase modulation is not. However, the two methods are so closely related that many of the frequency-modulated waves are produced by phase-modulation methods.