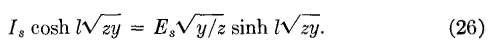Electromagnetic Wave Propagation

and

These equations can be written

and

since from the theory of hyperbolic functions

An examination of a table of hyperbolic functions will show that, when l = ∞, tanh lsqrt(zy) = 1.0; therefore, equations 27 and 28 become

and

where Z_s is the sending-end impedance of the infinitely long line considered, measured between the two line input terminals. If equations 29 and 30 are substituted in the general expressions 22 and 21, respectively, then

and

Since ε^-x = (cosh x - sinh x), these equations become

and

where

and is called the propagation constant per loop mile for the line under consideration. Like equations 21 and 22, these equations also give the voltage or current at any point along the line in terms of the sending-end values.